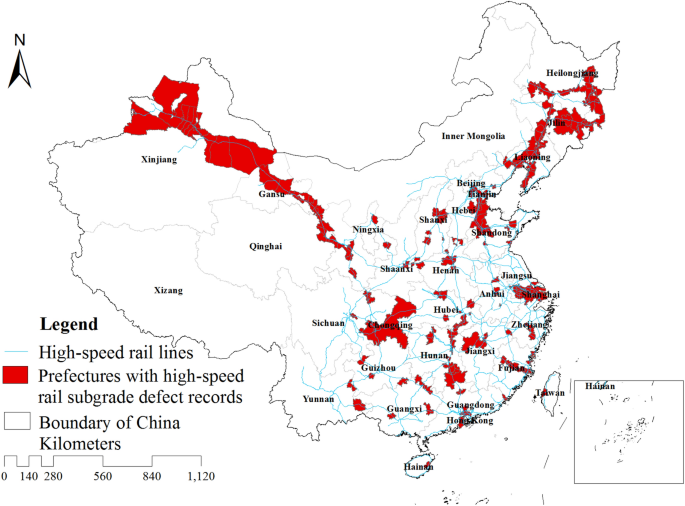
Historical HSR subgrade defect occurrences in China
We recently compiled an extensive georeferenced dataset of historical HSR subgrade17. The dataset was sourced from 24,735 peer-reviewed literature published from 1999 to 2022 in both Chinese and English, and a quality control procedure was applied to remove duplicates and ensure accuracy18,19. Subsequently, a total of 661 georeferenced event records of eight defect types were selected, crossing provincial, municipal, county, township, and smaller scales. Notably, subgrade settlement (settlement values ranging from 5 to 2300 mm), frost damage (frost heave values ranging from 4 to 50 mm), uplift deformation (ranging from 5 to 122 mm), and mud pumping exhibit the longest reporting history among the identified disease types. These definitions are detailed in Table 1. The distribution of HSR subgrade defect records across Chinese prefectural-level administrative regions is illustrated in Fig. 1.
The results indicate that the occurrence of these defects can be closely related to local climate and geological environment. For example, frost damage events are concentrated in the temperate zone of China, which is characterized by long and cold winters and high humidity throughout the year. The presence of pore water in the soil particles in the subgrade freezes and forms ice layers, resulting in soil displacement and subgrade frost heave. Mud pumping events are concentrated in the southeastern part of China, where frequent heavy rainfall occurs, causing a large amount of rainwater to infiltrate into the subbase and reduce its bearing stiffness. Under the high-frequency dynamic loads of trains, mud pumping and, in severe cases, subgrade settlement can occur. Subgrade swelling and upheaval are closely related to the slight expansion of the fill material used. Within the same climatic zone, multiple diseases often coexist, making the subgrade condition more complex.
Environmental driving factors
Climate variables
Average annual rainfall: Rainfall may alter the engineering properties of subgrade materials, thereby influencing the stability of the subgrade20.
Consecutive 5-day rainfall: This data serves as an index reflecting extreme rainfall21.
Number of days with maximum temperature exceeding 35 degrees celsius: This data can serve as an indicator reflecting extreme high temperatures16.
Annual freezing days: Annual freezing days quantify the number of days in a region where water freezes, and it is a key factor influencing the occurrence of frost damage on roadbeds15.
Wind speed: Strong winds may erode road shoulders, leading to a reduction in subgrade width, with sleepers/track panels exposed, thereby affecting the stability of the railway track22.
Geomorphological variables
Elevation: Elevation defines the highest and lowest points within a region and is reported to relate to the occurrence of various defects, such as, a number of defects have been reported on the Menyuan-Minle section of the Lanzhou-Urumqi HSR at high altitude15.
Slope and aspect: HSR subgrades may have varying slopes, resulting in different temperatures inside and outside the subgrade, potentially leading to uneven settlement23,24. The slope gradient may have an impact on the flow of moisture, thereby disrupting the drainage of the subgrade25.
Geohydrological variables
Rock hardness: Harder rocks can provide better support for HSR subgrade3.
Distance to fault: Geological faults provide pathways for groundwater and surface precipitation, which can affect subgrade26.
Soil texture: Subgrade defects can be associated with the types and properties of surrounding soil27.
Average distance to river: The presence of rivers increases the amount of groundwater in the surrounding geological environment, thus affecting the performance of subgrade28.
Average distance to lake: Lakes increase the amount of groundwater in the surrounding geological environment, which can impact the performance of subgrade8.
Anthropogenic variables
Land use: Land use indirectly influences the occurrence of subgrade defects. Extracting groundwater in urban areas can lead to subgrade defects, while areas with multiple rock types can enhance the strength of subgrade and reduce settlement29.
Average distance to road: Road construction, as a human activity, can have an impact on railway lines30,31.
Variable sources and preparation
The average annual rainfall, consecutive 5-day rainfall, number of days with maximum temperature exceeding 35 degrees Celsius, annual freezing days, and wind speed data were sourced from the National Earth System Science Data Center (http://www.geodata.cn/), with a spatial resolution of 0.25° and a time range from 2007 to 2016. We obtained annual average rainfall data through kriging spatial interpolation. The remaining factors were summarized within specified regions using ArcGIS’s zoning statistical function, displaying the data values in tabular form; Elevation data were obtained from the Geospatial Data Cloud (http://www.gscloud.cn) with a resolution of 30 m. Slope and aspect data at a 30 m resolution were derived using ArcGIS software’s slope function and aspect analysis tool; Land use data were sourced from the Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences (http://www.igsnrr.ac.cn), with an accuracy of 30 m. We calculated land use area within specified regions using ArcGIS’s zoning statistical function; The road, river, and lake data were extracted from OpenStreetMap. We calculated the average shortest distance from railway lines to these features using ArcGIS; Rock hardness and fault data were provided by the Geological Survey Cloud of the China Geological Survey Bureau (https://geocloud.cgs.gov.cn/). We categorized geological formations into different intervals to determine the average rock hardness within the region. The average shortest distance from railway lines to geological faults was calculated using ArcGIS. Soil texture data were sourced from the Harmonized World Soil Database (version1.2) (https://www.fao.org/home/en/), and we selected four soil attributes, including soil drainage capacity, soil composition, soil effective water storage capacity, and soil depth through filtering processes.
Methods
Data processing
The variables were standardized using the StandardScaler module, and the hyperparameters of the RF were optimized using grid search to build a screening model32. To streamline and enhance model performance, the recursive feature elimination method was used to remove the environmental variables with minimal contribution33,34. Specifically, a RF model was iteratively established 18 times, eliminating the least important environmental factors in each screening process based on their contribution. A criterion was set to prevent the incorrect elimination of important factors, ensuring that the contribution of the eliminated factors did not exceed 0.005. The adjusted remaining predictor factors were reintroduced into the model. Finally, 55 factors, out of the initial 73, for each type of defect were retained to construct the risk prediction model. All the factors are shown in Table 2.
Random forest modelling
The RF model is one of the most commonly used integrated algorithms in applied Machine Learning studies35,36. It utilizes repeated independent sampling to extract multiple samples from the original dataset and constructs decision trees for each sample. These decision trees are then aggregated and combined by voting, taking each decision tree as a member to achieve classification and prediction. In this study, the Random Forest algorithm emerges as a crucial tool in predicting the risk of subgrade defects in HSR infrastructure. Its capacity to process extensive datasets with various input variables and is robust against overfitting make it exceptionally suited for this task. Furthermore, as a non-parametric model, RF does not require assumptions about any specific form of relationship between variables, offering a significant advantage in examining the complex and not yet fully understood interplay between environmental factors and subgrade defects. Applying RF allows us to capture non-linear relationships and variable interactions that traditional statistical methods might overlook. Finally, RF is widely recognized and effective in identifying and determining variable importance. As a result, this approach has been successfully applied in the past for mapping landslides, debris flows, and many other types of disasters28,29,37.
RF calculates the decrease in Gini index \({D}_{Gk}\) by evaluating the evaluation factor k during node splitting. The importance of the evaluation factor k is determined by summing up \({D}_{Gk}\) of all nodes in the forest and taking the average over all trees. This measure represents the percentage of the average decrease in Gini index for the evaluation factor in relation to the total average decrease in Gini index for all factors. It is calculated according to Eq. (1):
$${P}_{K}=\frac{\sum_{h=1}^{n}\sum_{j=1}^{l}{D}_{Gkhj}}{\sum_{k=1}^{m}\sum_{h=1}^{n}\sum_{j=1}^{l}{D}_{Gkhj}}$$
(1)
where m, n, and l represent the total number of evaluation factors, the number of classification trees, and the number of nodes in a single tree, respectively. \({D}_{Gkhj}\) refers to the decrease in the Gini index of the jth node in the hth tree for the kth evaluation factor. \({P}_{K}\) denotes the importance level of the kth evaluation factor among all evaluation factors.
When constructing the RF models, the dataset was divided into a 7:3 ratio for training and validation. To enhance the robustness of model predictions and quantify the uncertainty, we employed an ensemble of 50 models trained on separate bootstraps of the dataset. The hyperparameters of each of the 50 individual models were determined using grid search, with random combinations of parameters, while all other tuning parameters were set to their default values. The combination with the highest average accuracy across the models was selected as the optimal parameter choice for the model. Furthermore, a five-fold cross-validation strategy was employed, whereby the training dataset was divided into 5 equal subsets, with 4 subsets used for model training and the remaining subset utilized for testing. This five-fold process was repeated iteratively, rotating the testing subset, in order to fully leverage all the training data for model training and testing while mitigating the impact of overfitting. To minimize the influence of randomness, each type of pathology was subjected to 50 models. Each one of these 50 models predicted the environmental risk on a continuous scale ranging from 0 to 1, and the final prediction graph was generated by calculating the average prediction across all models.
The model’s classification accuracy is analyzed using the Receiver Operating Characteristic (ROC) curve38,39,40, depicting the true positive rate on the vertical axis and the false positive rate on the horizontal axis. Greater accuracy in model classification is indicated by a higher true positive rate and a lower false positive rate. The ROC curve is generated by plotting the true positive rate (proportion of correctly identified defect samples) against the false positive rate (proportion of falsely identified non-defect samples).
Integrated risk map generation
The integrated HSR infrastructure risk assessment involves a holistic analysis that encompasses multiple subgrade defects that are most commonly reported in China, such as settlement, frost damage, uplift deformation, and mud pumping. This approach takes into account the cumulative impact of various factors—including climatic conditions, geomorphological features, geohydrological characteristics, and human activities—on the subgrade’s safety. In regions where the integrated risk scores are relatively high, an enhanced need for coordination and management emerges to effectively mitigate potential risk.
To quantify this integrated risk, we utilized the Random Forest (RF) model to evaluate the probability of each defect type occurring, averaging the outcomes across 50 iterations. Natural breakpoints were then utilized to divide each defect into four risk levels: low, low-medium, medium–high, and high28,41,42. Portions with average probability values greater than 0.6 for each defect were selected and assigned a value of 1; otherwise, they were assigned 0. Spatial coupling of the four defects was performed to produce a comprehensive risk map of railway subgrade defects in China The low, medium, high, and very high risk areas in the graph have values of 0, 1, 2, and 3, respectively, representing the risk level of the area.). It is noteworthy that this map displays regions with high risks for all four defects (probability values greater than 0.6), thus necessitating extra attention in HSR operations and new HSR planning. All distribution maps in the figure were drawn by ArcGIS (v10.7, www.esri.com).